Primer Lugar en el concurso de Carteles "Carlos Graef Fernández" del LXII Congreso Nacional de Física 2019

Dispersión de Hoyos Negros: Hayward

Resumen

Se hace un análisis sobre problemas de dispersión de ondas planas que incide en un agujero negro. En este trabajo en particular, se trabaja con un agujero negro de Hayward, utilizando la ecuación de Klein-Gordon para un campo escalar sin masa y se resuelve numéricamente la ecuación diferencial obtenida para encontrar la sección eficaz diferencial.

Introducción

Los agujeros negros son objetos tan compactos que ni siquiera la luz puede escapar de su atracción gravitacional. En la actualidad, la existencia de agujeros negros supermasivos (millones de veces la masa del sol) en el centro de muchas galaxias, y de agujeros negros más pequeños (5-10 veces la masa del sol) en sistemas binarios de rayos X es generalmente aceptada [1].

El agujero negro de Schwarzchild, es el más sencillo, posee simetría esférica y es descrito por el elemento de línea

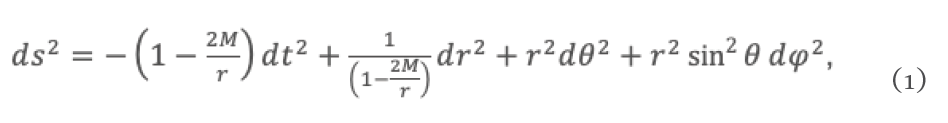
aquí, M es la masa del agujero negro (en unidades naturales).

En este trabajo, estudiaremos problemas de dispersión que involucren agujeros negros. Este problema es semejante a un problema de dispersión, donde el índice de refracción del medio no es constante. En el caso de los agujeros negros, la curvatura del espacio tiempo produce el efecto dispersivo de las ondas incidentes.

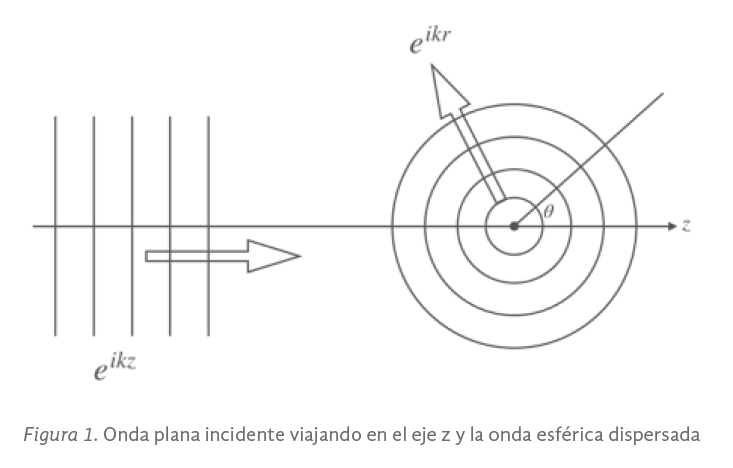
Consideremos una onda plana $\psi \left(z\right)=e^{{{}^i}^{\omega z}}$ que incide en el agujero negro. La información del agujero negro se encuentra codificada en un potencial efectivo de largo alcance. El efecto del potencial efectivo en la onda plana incidente modifica las expresiones estándar (espacio plano) para la amplitud de dispersión.

La onda dispersada (ver figura 1) puede ser expresada como

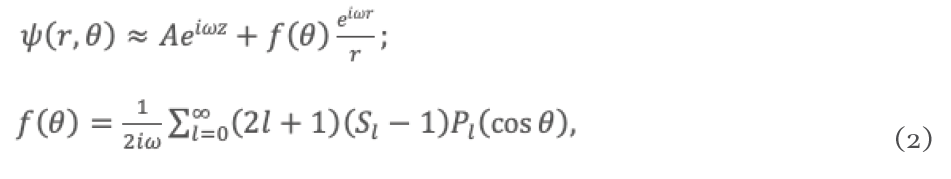
donde $f\left(\theta \right)$ es la amplitud de dispersión, $S_l$ es la matriz S y $P_l(cos\theta )$ son los polinomios de Legendre de orden l.

De la amplitud de dispersión, se obtiene la sección eficaz diferencial transversal [2], dado por

Ecuación de campo escalar y potencial efectivo

La referencia [3] describe un agujero negro regular, este modelo posee simetría esférica, es asintóticamente plano y no tiene singularidades en r = 0.

El elemento de línea del espacio-tiempo del agujero negro regular de Hayward es

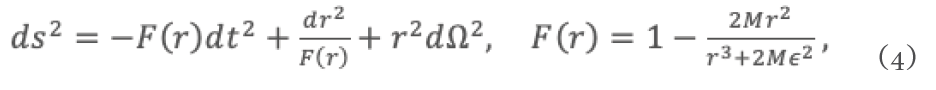
donde M representa la masa del agujero negro, el parámetro ε esta asociado a una constante cosmológica. Para ε = 0, la métrica de Hayward se reduce a la métrica de Schwarzschild.

El agujero negro regular de Hayward describe el comportamiento de un agujero negro que se está colapsando o que se está evaporando y puede tener uno o dos horizontes de eventos, dependiendo de la relación entre la masa y el parámetro ε.

Consideremos un campo escalar sin masa ψ que se propaga en el espacio tiempo de Hayward. La ecuación que gobierna la evolución del campo escalar es

Para ondas planas monocromáticas, tenemos

con ${\psi }_{\omega }=Y_l^m(\theta ,\phi )$ los armónicos esféricos. Substituyendo (6) en (5), se obtiene la siguiente ecuación

El potencial efectivo es graficado en la figura 2.

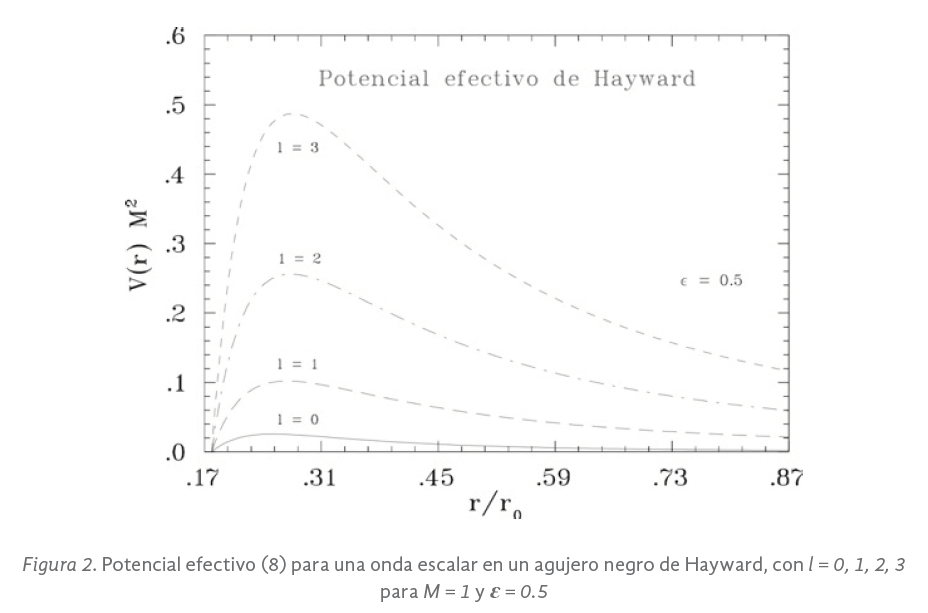
Solución numérica

La solución a la ecuación (7) es posible utilizando un método numérico, definiendo los valores de la función en cantidades discretas sobre una malla de espaciamiento nodal uniforme. La ecuación diferencial se convierte en una ecuación en diferencias finitas y puede ser resuelta a lo largo de una malla calculando nuevos valores de la función de valores conocidos previamente.

Utilizando la expansión de Taylor a segundo orden para una función u(r). Resolviendo para la primera y segunda derivada de u(r) (ecuaciones (3.5) y (3.26) de [4]) se tiene

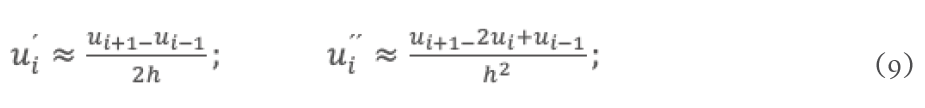
donde h es el intervalo entre los nodos y el subíndice en u etiqueta el punto nodal. Sustituyendo en la ecuación (7) y despejando $u_{i+1}$

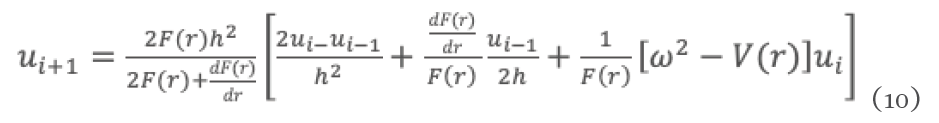
La amplitud de dispersión f(θ) puede reescribirse de la siguiente forma [4]

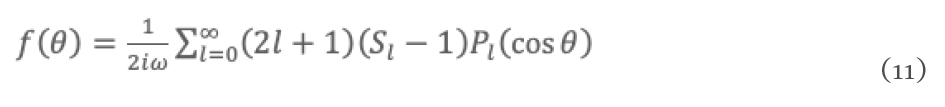
en donde $S_l$ recibe el nombre de matriz S. La cual está dada como

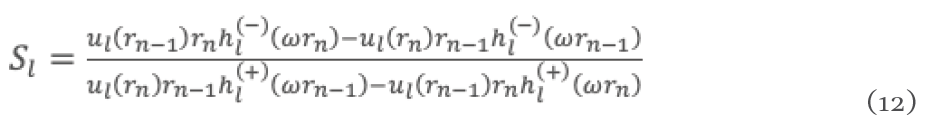
aquí $h_l^{(\pm )}\left(\omega r_n\right)$ son las funciones esféricas de Hankel y $u_l\left(r_n\right)$ son las soluciones de la ecuación (10).

Resultados

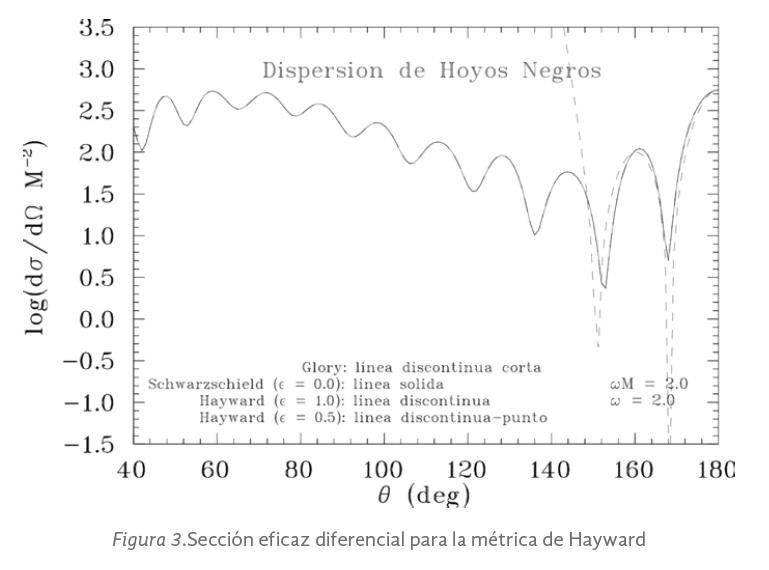
En la siguiente figura se muestra la sección eficaz diferencial de dispersión calculada numéricamente y la aproximación de Gloria.

Conclusiones y perspectivas

Referencias

ANEXO